Einstieg in das Thema
Was brauchst du als Basiswissen?
Du kennst Graphen, weißt, was das ist und
erkennst sie.
Worum geht es?
Um gut mit Graphen arbeiten zu können,
brauchen wir noch ein paar weitere Begriffe.
Diese sollen nun an Beispielen erläutert werden.
Was ist das Ziel?
Dein Wissen zu Graphen ist am Ende noch etwas
umfangreicher.
Erarbeitung
Aufgaben
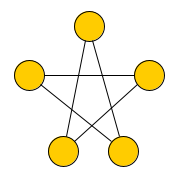
Aufgabe 1
Wie viele Nachbarn hat ein beliebiger Knoten in diesem Graphen?
Aufgabe 2
Von welchem Grad sind die Knoten?
Aufgabe 3
Wie viele Kanten ergeben sich, wenn man drei Knoten so verbindet, dass jeder Knoten mit jedem anderen Knoten verbunden ist? Zeichne dies auch!
Aufgabe 4
Wiederhole dies für vier und fünf Knoten. Zeichne und lies ab, wie viele Kanten man benötigt.
Aufgabe 5
Stelle eine Vermutung auf, viele Kanten man für sechs Knoten benötigt. Versuche dich an einer Begründung.
Aufgabe 6
Versuche eine allgemeine Formel oder Vorschrift für n Knoten aufzustellen.
Aufgabe 7
Gib den Grad der Knoten des obigen Bildes an.
Aufgabe 8
Bei 5 Knoten werden alle Knoten mit allen verbunden. Gib den Grad der Knoten an.
Aufgabe 9
Bei n Knoten werden alle Knoten mit allen verbunden. Gib den Grad der Knoten an.
Lass uns Mathe machen! Sicher kennst du Baumdiagramme aus der
Wahrscheinlichkeitsrechnung. Da steckt das Wort Baum ja schon drin.
Aufgabe 10
Kann ein solches Baumdiagramm Kreise haben?
Aufgabe 11
Wir gehen davon aus, dass eine Münze 1x geworfen wird. Zeichne das Baumdiagramm, ein Knoten ist am Anfang, zwei Knoten sind am Ende. Welchen Grad haben diese Knoten?
Aufgabe 12
Nun wird die Münze 2x geworfen. Welchen Grad haben der Anfang, die mittleren Knoten und die Endknoten?
Aufgabe 13
Wird sich der Grad der Knoten ("Start", "Ende" und "Dazwischen") ändern, wenn 3x oder 4x geworfen wird?
Stimmts? Suche Beispiele und prüfe die Aussagen.
Aufgabe 14
Ein Kreis hat immer genau so viele Knoten wie Kanten.
Aufgabe 15
In einem Kreis haben alle Knoten den Grad 2.
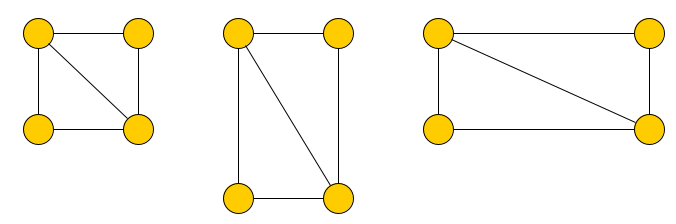
Aufgabe 16
Was sind wesentliche Unterschiede zwischen den drei Graphen?
Aufgabe 17
Dürfte man den Graphen auch noch anders zeichnen?
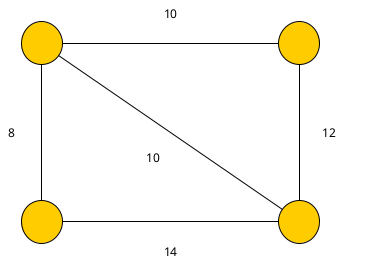
Aufgabe 18
Was sollen die Zahlen (wir nennen sie von jetzt an Kantengewichte) an den Kanten bedeuten?
Aufgabe 19
Ist dieser Graph noch mit den drei Graphen aus dem ersten Bild vergleichbar?
Aufgabe 20
Was passiert mit den Kantengewichten, wenn man einen Knoten an eine andere Stelle verschiebt?
Zusammenfassung
Was muss man wissen/können?
Du kennst Kantengewichte und den Grad eines Knotens,
kannst damit umgehen und hast Graphen in der Mathematik
wiedererkannt.
Was können anschließende Themen sein?
Es müsste eigentlich etwas Algorithmik reinkommen.
Aber das ist ein größeres Thema und mit einer Prüfung
sollst du zeigen, dass du die Grundlagen verstanden
hast.




